The many flavors of PID Algorithm
There are 3 different types of PID algorithm
- Ideal (also called "ISA")
- Series (also called "series" or "interacting" or "analog" or "classical")
- Parallel (also called "non-interacting", "independent" and "gain independent)
All 3 algorithms can achieve the same result theoretically; however the tuning constants to get that result may well be very different depending on the algorithm used.
You should be able to identify the algorithm used from the vendor-supplied instruction manual. To make identifying your particular algorithm a bit trickier, manufacturers vary on their names for these categories. They won't necessarily stick with the names on the list above.
The only way to really tell which algorithm you have is to look at the equation for the PID Controller. The equation may be written in the "classical" form or the "Laplace" form or as a block diagram. All 3 formats are shown in the following table to help you match it up with what's written in your user guide.
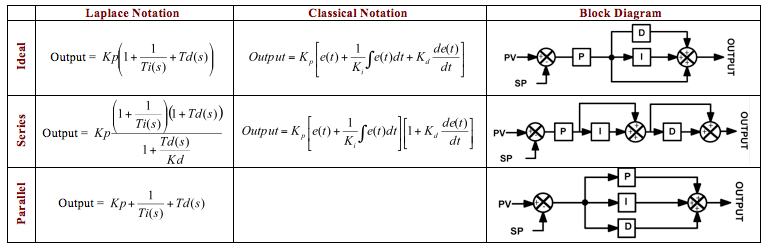
If your user guide does not make it clear which algorithm is being used – then fax the table above to the guy that sold you the controller and insist he sends it back with the row that contains your controller's algorithm circled.
Understanding the PID Algorithm differences
Don't be freaked out by the complex looking equations – to understand the difference between the algorithms, just look at the block diagrams.
The P, I and D blocks all do exactly the same function in isolation (which is described in detail in "The Complete Idiot's Guide to the PID Algorithm".
The difference between the algorithms is how the P, I and D gains affect each other. For example in the parallel algorithm, all 3 gains are totally independent, as the block diagram shows. That means that the P, I and D terms all act on a fresh, unadulterated error term, and then the results are combined (added) at the end.
In the series algorithm the output of the P goes into the I and then the D. For example, if your P gain was "2", then the I term would be multiplied by 2 as well before it did its integrating thang. And poor old D would act on the output of the integrator.
As you can probably imagine, performing trial and error tuning is a nightmare with series algorithms because you twiddle the P term and the I and D term all change too! Arrrgh! This pig's ear of an algorithm is a historical relic from the Pneumatic controller days when it was much cheaper to physically pipe up a series algorithm that the other two.
The Ideal algorithm isn't too bad. The only interaction is that the P term also scales the effect of the I and D terms.
To ensure that you get the right tuning constants first time, no matter which PID Controllers you need to tune, I recommend tuning your PID loop with a simple PID Simulation as your very first step on the road to loop tuning success.